우리는 자기장과 평행한 Two Fluid Plasma Wave의 Polarization에 대해서 다음과 같이 정의 했습니다.

n 굴절률에 따라 편광되는 방향이 달라집니다.

 일 경우  로 x방향의 전기장과 y방향의 전기장의 위상이 -i만큼 차이 나게 됩니다.

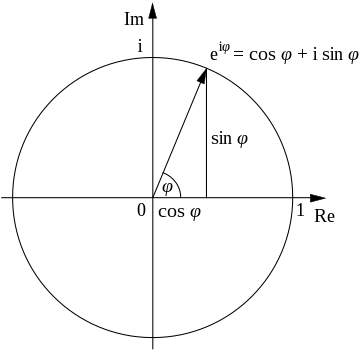
이것은 무슨의미 일까요? 먼저, 오일러 공식을 살펴보면

실수부와 허수부의 위상차이가 딱 90도가 나게 됩니다. 여기에 복소수를 곱하면 어떻게 될까요?

실수부가 cos이 sin으로 바꼇습니다. 위상이 90도 앞으로 가게 됬습니다. 그래서 위상이 i만큼 차이난다는것은 90도만큼 차이가 있다는것입니다.

다시 앞으로 가서,

일경우 이란 식이 나옵니다. 이것을 우리가 볼 수 있는 실수부만 보이게 하겠습니다.

(z=0 에서 봤을때 시간에 따른 R-mode polarization 전기장의 방향)

전기장이 반시계 모양으로 회전 합니다.

(Right-hand Polarization Wave)

일 경우

로 x방향의 전기장과 y방향의 전기장의 위상이 -만큼 차이 나게 됩니다.

(z=0 에서 봤을때 시간에 따른 L-mode polarization 전기장의 방향)

(Left-hand Polarization Wave)

 앞선 Two Fluid Plasma Wave 에선 전자의 주파수 영역을 다뤘다면, EMIC (Electromagnetic Ion Cyclotron) Wave에서는 Ion들의 영역을 다룰것 입니다. Ion의 특징은 전자보다 상당히 무거워서 Cyclotron 운동하는 속도도 상당히 느리다는것입니다. 그만큼 반응하는 Wave의 주파수 영역도 상당히 낮아지게 됩니다. 그래서 이제 우리는 상당히 낮은 주파수 영역을 다룰것입니다. 이런 수 들을 조금 더 다루기 쉽게 하기위해 식을 dimensionless quantity로 바꾸도록 하겠습니다.

 우리는 위의 식을 EMIC(Electromagnetic Ion Cyclotron) Wave에 적합한 식이 되도록 적당한 근사를 만들것입니다. 우선 Ion cyclotron frequency에 대해 다루기 때문에 Electron cyclotron frequency보다는 매우 작은 영역의 범위를 다루게 됩니다. 이런 조건을 가지고 적당한 근사를 만들 수 있습니다.

는 1이거나 1보다는 작은수를 다루게 되고, 전자파동에 비해 전자의 질량에 비해서 양성자의 질량이 1000배 정도 크기 때문에  입니다. 또 

는 1보다는 작은 영역을 다룰 것입니다. 즉 밀도가 자기장보다 큰 지역을 다루게 됩니다. 이는 일반 플라즈마 실험실과는 다른 우주에서 적용되는 근사입니다.

이렇게 작은 term은 0으로 처리하고 식을 근사 합니다. 그러면

 이를 토대로 Dispersion Relation을 계산하면,

(WNA=0 일때 Dispersion Relation)

(WNA=25 일때 Dispersion Relation)

WNA이 0도 일때와 0도가 아닐때 Dispersion Relation의 모양은 비슷해 보이지만 다른점은 그래프가 중간에 끊기는 지점이 나타난다는 것입니다. 먼저 Cut-off frequency를 계산해보면,

He과 O의 비율이 0이라면 분자의 해와 분모의 해가 같게 되서 분수가 꼴이 되어 해가 있을 수 없습니다.

이처럼 Cut-off frequency는 ion들의 비율에 따라 바뀌는것으로 계산되었습니다.

위의 Dispersion relation을 근사 시켜보도록 하겠습니다.

,이므로

그러므로 Cut-off frequency는 WNA과는 상관없고 오직 He과 O Ion의 구성 비율에만 상관이 있습니다.

(Multiful Plasma Polarization)

앞서 Polarization이 -i 면 R모드, i면 L 모드인 것을 계산 했었습니다. 위 그림은 Polarization의 복소수값을 plot한것인데요. 그래프에서 -값인 값들은 R모드이고, +값을 가르치는 값들은 다 L모드 입니다. 위 그림을 보시면 Polarization이 +값에서 -값, 혹은 -값에서 +값으로 바뀌는 지점이 있는데 그 지점을 Cross-over frequency라고 합니다. 바로 저 지점에서 전기장이 반시계 방향(R-mode)으로 돌다 반시계방향(L-mode)으로 혹은 반대로 돌게 됩니다. 25도일때 Dispersion relation을 보면 그래프가 갑자기 방향이 틀어지는 지점과 일치하기도 합니다.

이 Cross-over frequency를 수학적으로 계산하면 이 역시 Ion의 구성비율에만 관계가 있음을 알 수 있습니다.

 앞선 포스팅에서 Two Fluid Plasma Wave의 Dispersion Relation을 구해 봤는데요 이제 그의 물리적 의미를 살펴보도록 하겠습니다.

먼저 앞서 유도한 Dispersion Relation의 행렬식을 가져와 보겠습니다.

여기에서 이제 인 경우 즉, 파동의 방향이 자기장과 평행인 경우를 살펴보겠습니다. 파동의 방향이 자기장과 평행인 경우는 인 경우 입니다.

으로 정리가 됩니다. 이를 연립해서 정리하면.

으로 정리 할 수 있습니다. 이를 풀어보면

이렇게 파동의 굴절률(Index of reflection)을 정리할 수 있습니다. 이게 어떤 파동일까요? 특성을 알아 봅시다.

 맥스웰 방정식의 사용하지 않은 2개의 방정식으로 부터 전자기파의 특성을 볼 수 있습니다.

그리고

전기장의 z성분은 없으므로

전기장을 x성분과 y성분 그리고 파동으로 정의 할 수 있습니다.

 일 경우

 로 x방향의 전기장과 y방향의 전기장의 위상이 -i만큼 차이 나게 됩니다.

(Right-hand Polarization Wave)

일 경우

로 x방향의 전기장과 y방향의 전기장의 위상이 -만큼 차이 나게 됩니다.

(Left-hand Polarization Wave)

  일반적으로 직관으로 생각하면 위상이 i만큼 차이 난다는것은 90도 만큼 차이나는 것을 뜻합니다.

 이것을 잘보면 Right-hand Polarization Wave는 전자의 gyro motion 방향과 일치하고 Left-hand Polarization Wave 이온의 gyro motion 방향과 일치 합니다. 나중에 보면 이 회전하는 전기장이 전자나 이온과 공명(Resonence)를 일으켜 에너지를 전달하게 됩니다.

그럼 이제 만약 굴절률이 -(Negative)가 되면 어떻게 될까요?

파수(Wave Number)가 Complex Number로 나왔습니다.

지수 부분이 공간적으로 decaying되는 solution이 나왔습니다.

(damping 되는 파동)

어짜피 없어지는 파동이기 때문에 굴절률이 -인 파동은 다루지 않습니다.